Suunto PM5 Manuel utilisateur

La page charge ...

4

PM-5/1520

ALTIMÈTRE OPTIQUE

L’altimètre PM-5/1520 de Suunto est un instrument destiné à mesurer des hauteurs

et plus particulièrement des hauteurs d’arbres, avec précision et rapidité. Le corps de

l’instrument est en aluminium anodisé résistant à la corrosion. Le disque gradué

repose sur un palier spécial dans une capsule en plastique étanche et toutes les

parties mobiles sont immergées dans un liquide, ce qui permet au cadran de se

déplacer librement et de s'arrêter rapidement. Le liquide ne gèle pas, conserve

l’ensemble de ses propriétés d’amortissement dans des conditions de travail et

élimine les vibrations irritantes de la calamine.

MODE D’EMPLOI

En cas de mesure d’une hauteur à une distance de 15 ou 20 mètres, trois hauteurs

peuvent être lues directement sur l’échelle de l’altimètre. En cas de mesure d’une

hauteur à une distance de 30 ou 40 mètres, le chiffre obtenu doit être doublé.

L’altimètre de Suunto peut également être utilisé pour déterminer l’angle d’une pente.

Pour ce faire, il convient de visualiser la ligne de la pente à l’aide de l’échelle de

20 mètres à gauche de l’instrument. Le relevé obtenu permettant d’obtenir l’angle

peut être comparé aux chiffres indiqués dans le tableau de conversion situé à l’arrière

de l’instrument.

5

MESURE DES HAUTEURS

La mesure réelle de la hauteur de

l’arbre doit être réalisée depuis la

distance mesurée comme suit :

l'observateur vise la cime de l’arbre en

gardant les deux yeux ouverts. L’objet

observé, le réticule et l’échelle

apparaissent simultanément dans le

champ de vision de l’instrument. Dès

que le réticule coïncide avec la cime

de l’arbre, la hauteur de ce dernier

peut être lue (dans cet exemple, à

partir de l’échelle de 20 m à gauche

de l'instrument). La lecture obtenue

correspond à la hauteur de l’arbre

mesurée à hauteur des yeux de

l’observateur. La base de l’arbre n’est

pas observée. Si elle se trouve sous

la hauteur des yeux de l’observateur,

la hauteur réelle de l’arbre est

obtenue en cumulant les deux

relevés. Si elle se trouve au-dessus

de la hauteur des yeux de

l’observateur, la hauteur de l’arbre est

obtenue en calculant la différence

entre les deux relevés. En fait, dans le

6

dernier cas, la distance ne peut pas être mesurée horizontalement. Par conséquent,

pour obtenir le résultat exact, il convient de procéder comme suit : sur un sol plat, les

lectures supérieures de l’arbre suffisent généralement : il suffit d’ajouter la hauteur au

niveau des yeux de l’observateur (1,60 m dans ce cas), qui est déjà connue.

MODE D’EMPLOI DU NOMOGRAMME

Si, en raison d’un terrain irrégulier, la

distance ne peut pas être déterminée

horizontalement comme indiqué ci-dessus,

le nomogramme de la page 7 doit être

utilisé.

DÉTERMINATION DE LA DISTANCE DE BASE

Étant donné que cet instrument ne comporte pas de prisme, la distance de base, par

exemple 15 mètres, doit être mesurée à l’aide d’un ruban d’arpenteur. Prendre les

lectures du sommet et du pied et additionner ou soustraire ces valeurs pour obtenir la

hauteur apparente. Sur le nomogramme de la page 7, chercher la hauteur apparente

sur l’échelle de droite. Sur l´échelle double de gauche, chercher la lecture obtenue en

visant le pied de l´arbre. Noter que les lectures des gradients doivent être prises de

côtés différents de l’échelle. Relier ces deux points du nomogramme par une ligne

droite. L’échelle centrale du nomogramme indique désormais la hauteur réelle de

l'arbre.

7

Remarque importante

Les axes optiques des yeux de certaines

personnes ne sont pas parallèles. Ce

phénomène s’appelle hétérophorie. Il peut

varier avec le temps et dépend également

de plusieurs facteurs. Par conséquent,

afin de s´assurer que ce phénomène

n’affectera pas la précision des lectures, il

est conseillé à l’utilisateur de contrôler sa

vue, avant la lecture, en faisant le petit

test suivant : commencer par effectuer

une lecture en gardant les deux yeux

ouverts, puis fermer l’œil libre. Si les

lectures ne divergent pas

considérablement, c’est que les axes

optiques sont alignés, et les deux yeux

peuvent donc être tenus ouverts pour

prendre des lectures. Si les lectures

diffèrent, tenir l’autre œil fermé et viser à

mi-chemin en direction du côté du corps

de l´instrument, afin de créer une illusion

optique, grâce à laquelle le réticule se

prolonge au-delà du corps de l'instrument

et est visible contre l'objectif.

16

15

14

13

12

11

10

9

8

7

6

5

4

3

2

1

0

21

20

19

18

17

16

15

14

13

12

11

10

9

8

7

6

5

4

2

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

m

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

m

L-20

m

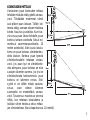
Terrain mountant

Lecture à la base

Hauteur corrigée

Hauteur apparente

Terrain déclinant

8

PM-5

CLINOMÈTRE À LECTURE OPTIQUE

Le CLINOMÈTRE de poche SUUNTO est solide, ce qui

permet de l’utiliser pour tout type de travail. Grâce à sa

lentille exempte de parallaxe intégrée au design, il

permet une lecture facile et rapide.

La visée et la lecture s’effectuent simultanément.

L’instrument ne comporte ni vis de fixation, ni niveau, ni

besoin de réglage.

En cas d’espace restreint, comme dans les travaux

géologiques et minéralogiques, les déclivités et autres

formations peuvent être déterminées en plaçant

l’instrument le long du contour ou de la surface de la

formation ; l’angle est ensuite lu directement à travers

la fenêtre latérale.

Caractéristiques de la construction

La structure est en aluminium léger résistant à la

corrosion.

Le disque gradué est soutenu par un ensemble de

paliers à rubis et toutes les pièces mobiles sont

immergées dans une capsule en plastique hermétique et très solide remplie de

liquide amortisseur. Le liquide amortit toutes les vibrations excessives de l’échelle et

permet un mouvement en douceur et sans à-coups du disque gradué.

Le matériau du conteneur n’est pas agressé par le soleil ou l'eau. Le liquide ne gèle

pas dans les conditions arctiques et ne s'évapore pas sous les tropiques.

Graduation

en % +/-

Graduation

en degrés +/-

Prolongement

du réticule dû

à l'illusion

optique

Graduation com-

plémentaire en

degrés de la fe-

nêtre latérale

9

Caractéristiques techniques

Poids : 120 g Dimensions : 74 x 52 x 15 mm. Les échelles optiques sont graduées en

degrés, de 0° à ±90° et de 0 % à ±150 %.

Une table de cosinus est imprimée au dos de l’instrument.

Résolution

Elle peut être lue directement selon une précision de 1 degré ou 1 %. Elle peut être

estimée avec une précision de 10 minutes ou env. 1/5 de 1 %, ce dernier chiffre

s’appliquant naturellement aux lectures autour de zéro.

VERSIONS DE PM-5 DISPONIBLES

Le PM-5/360 PC de base a été développé en plusieurs variantes dotées de

différentes combinaisons de graduation pour des usages spéciaux. Par conséquent,

une version comportant une graduation de ”nouveaux degrés” ou grades est

maintenant disponible. Ici, plutôt que d’observer la division normale en 360 degrés, le

cercle complet est divisé en 400 grades (g). La graduation en pourcentage est

normale. Le modèle concerné est le PM-5/400 PC.

10

MODE D’EMPLOI

Les mesures s’effectuent généralement à l’aide de l’œil droit. En raison des

différences d’acuité visuelle et des préférences personnelles, il est parfois plus facile

d’utiliser l’œil gauche. Il est de la plus haute importance de garder les deux yeux

ouverts. La main soutenant l’instrument ne doit pas gêner la vision de l’autre œil.

Tenir l’instrument devant l’œil qui effectue la lecture, de sorte que la graduation soit

lisible à travers l’optique et que la fenêtre latérale ronde soit orientée vers la gauche.

Orienter l’instrument vers l’objet en le soulevant ou en l’abaissant jusqu’à ce que le

réticule soit visible sur le point à mesurer. Parallèlement, lire la position du réticule sur

l’échelle pour obtenir la mesure. En raison de l’illusion optique, le réticule (pointeur en

croix) semble se prolonger au-delà du cadre et peut donc être observé facilement sur

le terrain ou l’objet.

La graduation à gauche indique l’angle de la pente en degrés depuis le plan

horizontal à la hauteur des yeux. La graduation de droite indique la hauteur de

l’objectif depuis la même hauteur horizontale des yeux et elle est exprimée en

pourcentage de la distance horizontale. L’exemple suivant illustre la procédure.

11

La tâche consiste à mesurer la

hauteur d’un arbre situé à une

distance de 25 m / 82 pi. sur un sol

plat. L’instrument est incliné, de

sorte que le réticule soit visible

contre la cime de l’arbre (sommet).

La lecture obtenue est 48 %

(environ 25,5°). Comme la distance

est de 25 m / 82 pi., la hauteur de

l’arbre est de 48 / 100 x 25 m = env.

12 m, soit 48 / 100 x 25 m = env. 12

m, soit 48 / 100 x 82 pi. = env. 39 pi.

À ce chiffre doit être ajoutée la

hauteur des yeux depuis le sol, par

ex. 1,6 m ou 5 pi.½. La somme de

ces chiffres est 13,6 m, soit 44 pi.

½, ce qui correspond à la hauteur

de l’arbre.

En cas de mesures très précises et

en particulier sur un sol en pente, deux relevés sont réalisés, le premier au sommet et

l'autre à la base du tronc. Lorsque la base du tronc se trouve sous la hauteur des

yeux, les pourcentages obtenus sont ajoutés. La hauteur totale correspond au

pourcentage total de la distance horizontale. Par exemple, si la lecture du sommet est

41 % et la lecture du sol 13 %, la hauteur totale de l’arbre mesurée à une distance de

25 m / 82 pi. est (41 + 13) / 100 x 25 m = 54 / 100 x 25 m = env. 13.5 m, soit (41 + 13)

/ 100 x 82 pi. = 54 / 100 x 82 pi. = env. 44 ½ pi.

12

Lorsque la base du tronc se situe au-dessus de la hauteur des yeux, la lecture de la

base est soustraite de la lecture du sommet et la hauteur totale correspond à la

différence en pourcentage de la distance horizontale.

Par exemple, si la lecture du sommet est 65 % et la lecture de la base 14 %, la

hauteur totale est (64 – 14) / 100 x 25 m = 50 / 100 x 25 m = 12,5 m, soit (64 – 14) /

100 x 82 pi. = 50 / 100 x 82 pi. = 41 pi. Pour des raisons de simplicité, lorsque les

calculs sont réalisés mentalement, il est conseillé d’utiliser une distance de 50, 100

ou 200 m / pi.

Tous les relevés sur l’échelle des pourcentages sont effectués à partir de la distance

horizontale. Cela signifie que si la distance d’un terrain en pente est mesurée au sol,

une erreur est insérée et doit être corrigée pour que les résultats soient corrects.

Cette erreur est peu importante dans la plupart des cas lorsque les angles sont

faibles mais elle augmente progressivement lorsque l’angle s’accentue.

13

La corrélation trigonométrique est la suivante :

H = h x cos

α

où H est la hauteur réelle ou corrigée, h la hauteur observée et α (alpha) l’angle de la

pente au sol. À l’aide de l’équation précédente, il est également possible de procéder

à la correction à distance. Dans ce cas, h correspond à la distance mesurée au sol et

H à la distance horizontale recherchée. Si la distance corrigée est utilisée, il n’est pas

nécessaire de corriger la hauteur observée. Lors du calcul de la distance horizontale

à l’aide de la distance au sol et de la pente, il convient de préciser qu’une erreur est

insérée si la pente est mesurée depuis la hauteur des yeux jusqu’à la base du tronc.

Il serait gênant et non pratique de mesurer la pente au sol. Toutefois, aucune erreur

n’est insérée lorsque l’angle de la pente est mesuré depuis la hauteur des yeux

jusqu’au repère indicateur réalisé ou placé sur le tronc à la hauteur des yeux, les

deux lignes de la mesure devenant parallèles. L’angle réel de la pente est de 9

degrés.

L’exemple indiqué sur la figure

suivante illustre les deux

méthodes de calcul.

1ère méthode : mesurer la

distance au sol. Elle est égale à

25 m / 82 pi. Ensuite, mesurer

l’angle de la pente. Il est de 9

degrés. Lire les pourcentages

des points situés au niveau de la

cime et du sol. Ils sont de 29 et

23 %.

14

Calculer :

Prendre 52 % de 25 m / 82 pi. Cela correspond à 13 m / 42,6 pi. Multiplier ce chiffre

par le cosinus de 9 degrés.

0,987 x 13 m = 12,8 m, soit 0,987 x 42,6 pi. = 42 pi.

2ème méthode : multiplier la distance au sol par le cosinus de l’angle de la pente.

0,987 x 25 m = 24,6 m, soit 0,987 x 82 pi. = 80,9 pi.

Ajouter le relevé des pourcentages comme indiqué ci-dessus et prendre la somme

des pourcentages de la distance corrigée.

soit

Cet exemple indique qu’un angle de 9 degrés entraîne une correction de 2,3 %

seulement mais lorsque l’angle est de 35 degrés, la correction correspond à une

réduction d’environ 18 % de la hauteur observée.

23

100

-------- -

29

100

-------- -

52

100

-------- -=+

52

100

-------- -

24 6m 12 8m,=,×

52

100

-------- -

80 9ft 42ft=,×

15

CORRECTION DE LA HAUTEUR NOMOGRAPHIQUE

En cas d’utilisation du nomogramme, il devient inutile de calculer toutes les

corrections. Seule une règle ou un autre objet pratique muni d’un bord droit est

nécessaire pour obtenir la solution nomographique. Pour utiliser le nomogramme,

placer la règle de sorte que son bord coupe l’échelle de l’angle à gauche au niveau

du point de l’angle de la pente et l’échelle de la hauteur observée (à droite) au niveau

du point pertinent. La hauteur (ou distance) corrigée est lue au point où le bord coupe

l'échelle de hauteur corrigée au centre. En cas d’utilisation d’une distance de 100 m/

pi. au sol, la procédure de correction est très simple. Il est alors inutile de mesurer

l'angle de la pente. Il suffit de lire le relevé du point au sommet et du point au sol.

Selon la situation, leur somme ou différence indique la hauteur apparente

directement en pieds. Elle est ensuite corrigée comme suit : tout d’abord, chercher le

point indiquant la hauteur apparente sur l’échelle de droite dans le nomogramme.

Ensuite, chercher le point indiquant le relevé du point au sol sur l’échelle double de

gauche. Enfin, relier ces points. Le relevé corrigé est déterminé à partir de l’échelle

moyenne pertinente au point d'intersection. Dans cette procédure, l’angle de la pente

peut être négligé car l’échelle du point au sol à gauche a été réalisée de sorte que

l’angle de la pente et la hauteur moyenne des yeux de 1,6 m / 5,5 pi. soient pris en

compte.

16

PROTECTION DU CORPS DES KB-14 ET PM-5 DE SUUNTO

La protection du corps de l'instrument convient aux modèles KB et PM suivants :

KB-14 (tous les modèles) et PM-5.

La page charge ...

Suunto PM5 Manuel utilisateur

Ce manuel convient également à

Suunto PM5 Manuel utilisateur

dans d''autres langues

Documents connexes

Autres documents